Simulation Results

We have already said that sequential least squares has conditioning problems for cruising flight, and in the simulations, it did not disappoint.

Each simulation starts out from a trimmed condition. With no noise, no control input, and using the known model, the airplane would fly straight and level forever. Every simulation initialized the parameters to their known values. Also, every simulation added Gaussian noise to the variables used in the controller and estimator.

The simulations could be run with different forgetting factors and sampling rates for the parameter identification. Some of the simulations modeled damage to the elevator occuring at $t=200\textrm{ s}$. Its effectiveness was halved by adjusting the appropriate values in the known parameter vector. Some simulations modeled a pullup manuever at $t=800\textrm{ s}$, followed by an opposite push-down maneuver 10 seconds later.

The first few simulations, however, were straight and level throughout. Figure 3 shows the simulation with $\lambda =0.99$ and a least squares update rate of 100 times per second. It only took about 11 seconds for the parameters to blow up.

Figure 3: Time history of the parameter $m_2$, for $\lambda =0.99$.

Knowing that increasing $\lambda$ can improve conditioning, at the expense of transient performance, I tried $\lambda =0.999$. This time the parameters lasted almost 100 seconds before blowing up, as seen in Figure 4.

Figure 4: Time history of the parameter $m_2$, for $\lambda =0.999$.

It seems logical to just eliminate the forgetting factor altogether. Figure 5 shows the percent error for the six of the parameters, for a simulation run with $\lambda=1$. The change in values of all parameters remained well under one percent for the 20 minutes simulated.

Figure 5: Time history of all the $C_M$ parameters, for $\lambda =1.0$ (no forgetting factor).

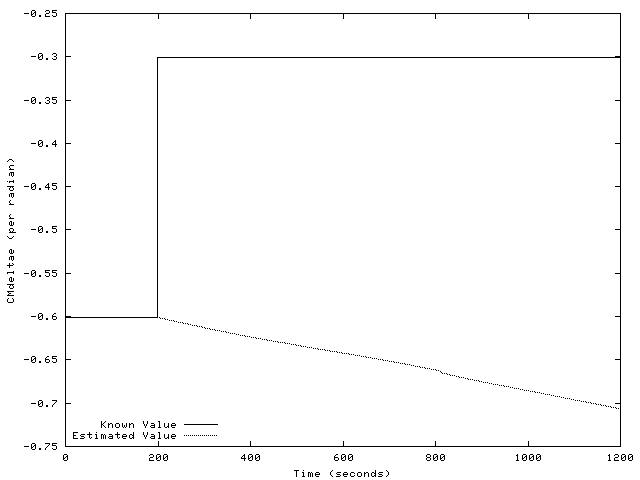
Having found a configuration where the parameters do not blow up, let us look at its response to some damage sustained by the control. Figure 6 shows the known and estimated values of one parameter, $m_2$. At $t=200\textrm{ s}$, the damage occurs, resulting in the halving of the known parameter's value. The estimate stays near the known value until the damage occurs. But, curiously, after the damage, it moves away from the new known value.

Figure 6: Time history of the parameter $m_2$, along with its known value, for $\lambda =1.0$. At $t=200\textrm{ s}$, the elevator effectiveness dropped by half.

How does this affect performance? Figure 7 shows the pitch-rate of a pull-up maneuver performed ten minutes after the damage occured, along with the commanded rate. The performance is very good, even though the estimated parameters are significantly different from the known values. This is no doubt due to a hardy feedback control; yet it tells us that a good feedback control can compensate for a poor system model quite well. For comparison, Figure 6 shows the same pull-up maneuver performed with no damage to the elevator. There is hardly any apparent difference in their performances.

Figure: Time history of the command and actual pitch rates, around $t=800\textrm{ s}$, when a pullup maneuver occured. The conditions here the same as for Figure 6.

Figure: Time history of the command and actual pitch rates, around $t=800\textrm{ s}$, when a pullup maneuver occured. In this case, there was no damage to the elevator. $\lambda =1.0$.

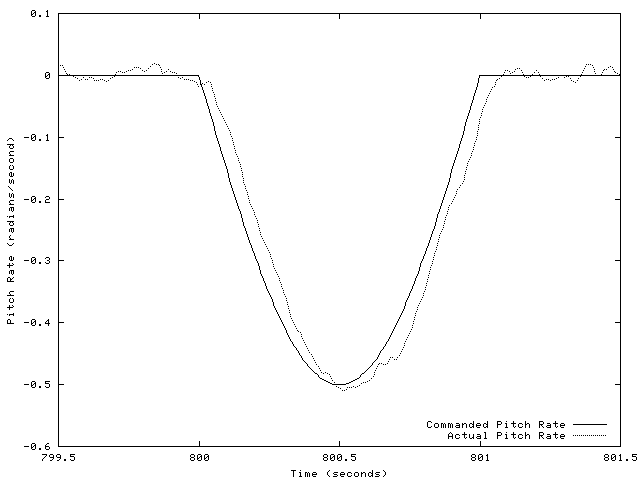
When faced with the problem of poor conditioning in the estimator, we previously attempted to remedy it by increasing (and ultimately eliminating) the forgetting factor. Although the airplane performed its maneuver well, the parameter estimates were unacceptable. At some point, having accurate parameters will be crucial, and a forgetting factor will be necessary for that.

Therefore, we try another remedy for the conditioning problem: decreasing the least squares update rate. The rationale for this is that increasing the time between updates gives the airplane more time to change its state. Too many samples with the nearly the same input is what causes the conditioning problem, so increasing the sample time could reduce the number of similar inputs. (I also suspect there may have been some interactions between the simulation and the estimator due to discrete effects; changing the

In any case, in following simulations, the forgetting factor was set to 0.99, while the estimator was only updated once every ten time steps (ten times per second). Indeed, as Figure fig:case6-param show, the parameters ($m_2$, at least) do not blow up. In fact, after damage occurs, they migrate to the new value. (That is, the estimator does what it's supposed to do.)

Figure 9: Time history of the parameter $m_2$, along with its known value, for $\lambda =0.99$, but at a lower sampling rate. At $t=200\textrm{ s}$, the elevator effectiveness dropped by half.

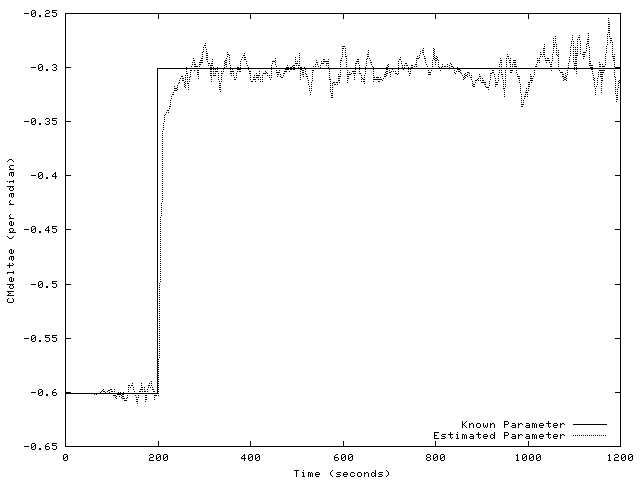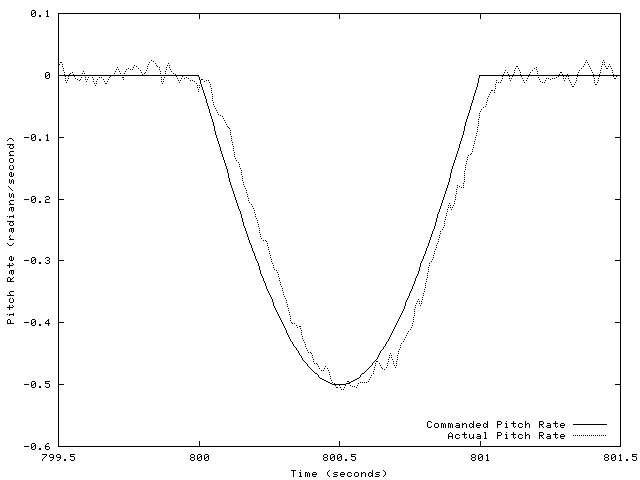
Figure 10 looks briefly at the control system performance under these conditions. The performance is mostly quite good.

Figure: Time history of the command and actual pitch rates, around $t=800\textrm{ s}$, when a pullup maneuver occured. The conditions are the same as for Figure 9.

An interesting feature of this Figure 10 is the temporary divergence towards the end of the maneuver. I suspect the reason for this is that, during the manuever, certain poorly estimated parameters come to dominate. While the airplane is cruising, it can collect no data for high angles of attack. Thus, parameters that dominate at high angles of attack would not get identified as well. When a high angle of attack is suddenly encountered in the pull-up, an ill-estimated parameter could cause the divergence.

One signifant fact about the previous simulation is that its the success depended on a certain amount of noise present. When the simulation was run with less noise, the parameters once again blew up.