Dynamic Modeling

Stability is a dynamics problem, and so we must begin by modeling the dynamics of the helicopter. We do this using Newtonian mechanics. The equations of motion relate the helicopter motion to the forces exerted on it. Thus, dynamic modeling boils down to determination of the forces and moments.

Several assumptions can be made to simplify the analysis. The major assumptions are stated here.

• The helicopter is a rigid body, symmetric about its longitudinal plane.
• The transients of the rotor flapping motion are insignificant; when anything affecting the blade flapping changes, the blades are assumed to react immediately. This is the quasi-steady assumption.
• The induced inflow approximately varies linearly across the disk. In particular, the induced inflow is a linear function of distance downwind of the upwind tip.
• For helicopters, the tip speed is fixed. For autogyros, the tip speed is set to zero the rotor torque.
• Blade stall is ignored, as are tip effects and the effects of the reverse flow region.
• Blades are teetering (i.e. no hinge offset). This is perhaps not a good assumption, but the unbelievable simplification it allowed made me willing to accept it.

Rigid-Body Equations of Motion

The derivation of the rigid body equations of motion are beyond the scope of this report. The basis of the derivation is Newton's Second Law, in linear form ( $\vec F=m\vec a$) and angular form ( $\vec M=\Vec{\Vec I}\vec\omega$). Newton's law is applied to the force and moment resolved into body axes, taking Coriolis and gravity forces into consideration.

Simplifying, using the symmetry assumption, and solving for the accelerations, yield:
  $$\begin{align}\dot u & = rv - qw + \frac Xm - g\sin\Theta \\ \dot v & = pw - ru ... ... \dot r & = (I_{xz}\dot p - (I_{yy}-I_{xx})pq - I_{xz}qr + N)/I_{zz} \end{align}$$

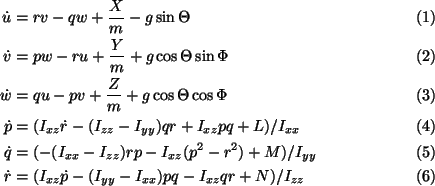
While the Coriolis and aerodynamic forces in Equations 1-6 are functions of the velocities and angular velocities ($u$, $v$, $w$, $p$, $q$, $r$), the gravity terms are functions of two Euler angles, $\Phi$ and $\Theta$. Thus, the system is not yet closed.

Equations 7 and 8 relate the Euler angle rates to the angular velocities.
  $$\begin{align}\dot\Phi & = p + q\sin\Phi\tan\Theta + r\cos\Phi\tan\Theta \\ \dot\Theta & = q\cos\Phi - r\sin\Phi \end{align}$$
These make $\Phi$ and $\Theta$ state variables, forming a closed system of eight equations with eight state variables.

In the above equations, only the aerodynamic forces and moments ($X$, $Y$, $Z$, $L$, $M$, $N$) are unknown. They are functions of the state variables, as well as the control variables. The next two subsections detail their calculation.

Rotor Forces and Moments

The rotor forces are functions of the following:

• State variables: $u,v,w,p,q,r$
• Rotor collective and cyclic pitch: $\theta_0,\theta_{1s},\theta_{1c}$
• Induced inflow: $v_i$
• Flap angles: $\beta_0,\beta_{1c},\beta_{1s}$
• External downwash

Only the state variables and the rotor collective and cyclic pitch are known. The others must be calculated.

Rotor Axes

The calculation of rotor forces take place in shaft axes, where the $z$-axis is collinear with the shaft of the rotor. Although control axes use (much) simpler equations for in-plane forces, the control axes are not fixed with respect to the helicopter fuselage. This introduces bookkeeping problems. The shaft axes are fixed, and so a fixed transformation can be used to transform vectors from body axes to shaft axes.

The calculation of forces actually occurs in shaft-wind axes, which is a rotation of the shaft axes so that the $x$-axis points directly into the wind. In shaft-wind axes, the $y$-component of velocity is zero by definition, which simplifies the equations somewhat. Variables in shaft-wind axes are denoted by a subscript $w$.

For example, to transform the angular velocity components from body axes to shaft-wind axes, one would use the relation

$$\begin{Bmatrix}p_w \\ q_w \\ r_w \end{Bmatrix} = \begin{bmatr... ...~ & ~ & ~ \end{bmatrix}\begin{Bmatrix}p \\ q \\ r \end{Bmatrix}$$

where $[C_{BS}]$ is the fixed body-to-shaft rotation matrix and $\psi_w$ is the angle between the shaft and shaft-wind $x$-axes. Velocity, angular velocity, cyclic pitch, and flapping angles must all be transformed to shaft-wind axes for rotor calculations. The force and moment determined by the calculation is transformed back to body axes afterwards by the inverse transformation.

Induced Flow

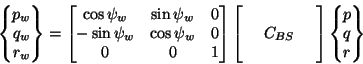
Calculation of the induced inflow requires the thrust of the rotor. Unfortunately, thrust is the ultimate goal of this calculation, so it is unknown. An iterative calculation is required. In Section 3, we will see that the trim solution also requires iteration. Therefore, we calculate $v_i$ based on the expected thrust at the trim condition, which, when the trim iteration converges, will be the actual thrust produced by the rotor. For the main rotor, this is the helicopter's gross weight. For the tail rotor, it is the amount of thrust needed to offset the main rotor torque.

Once the expected thrust, $T_e$, is known, the induced downwash can be calculated using Equation 9.

$$v_i = \begin{cases} \displaystyle \sqrt{\frac{T_e}{2\pi R^2\r... ...tyle \frac{T_e}{2\pi R^2\rho V} & \quad V > v_i \\ \end{cases}$$ (1)

This relation is not accurate for airspeeds near $v_i$; furthermore, the function is not differentiable at $V=v_i$ (which can possibly cause difficulties in the trim iteration). The relation can be improved by ``fairing'' the function near $V=v_i$ using empirical data.

Flapping

The quasi-steady assumption means that flapping transients are ignored. Thus flapping is a function of the rotor velocity and angular velocity, the induced inflow, and the collective and cyclic pitches.

To facilitate calculation of the flapping, the typical dimensionless ratios are defined:
$$\begin{align*}\mu &= \frac{u_w}{\Omega R} & {\bar p}_w &= \frac {p_w}\Omega \\ ... ...bda &= \frac{w_w - v_i}{\Omega R} & {\bar q}_w &= \frac {q_w}\Omega \end{align*}$$

There three flapping angles are the coefficients of a first harmonic expansion of the flapping as a function of azimuth:

$$\beta \approx \beta_0 + \beta_{1c}\cos\psi + \beta_{1s}\sin\psi$$

Note that the sign convention for $\beta_{1c}$ and $\beta_{1s}$ is the opposite as used in Glessow and Myers. (Padfield was inconsistent about the flapping sign convention, leading to several implementation headaches.)

The relations for flapping are simplified (and corrected) versions of those given by Padfield (page 107):
$$\begin{align*}\beta_0 =& \frac\gamma8 \bigg[\theta_0\left(1+\mu^2\right) + \th... ...-{\bar p}_w\left(\frac{16}\gamma\right)\left(1-\frac{\mu^2}2\right) \end{align*}$$

Force and Moment

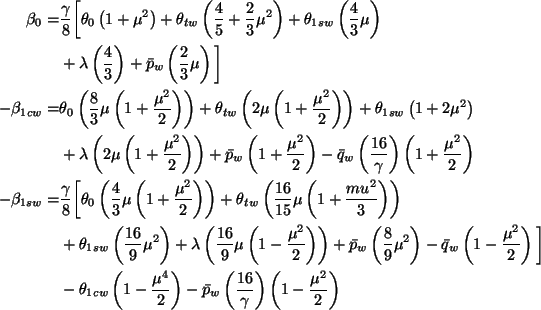
Once the flapping angles have been determined, the force and moment can be calculated. The calculation of force is a straightforward, albeit long, calculation. The equations for force are taken directly from Padfield, pages 110-111, and the moment equations come from pages 114-115. They are much too long to reproduce here.

Fuselage and Empennage Forces and Moments

Fuselage forces are difficult to calculate. Typically, empirical data is used. When less accuracy is needed, such as for student projects, there are rough approximations based on empirical testing in most aircraft aerodynamics textbooks.

For this report, I used rough estimation formulas from McCormick. The fuselage drag coefficient (based on frontal area $A_F$) is a function of slenderness ( $\ell/A_F^2$) and for this calculation is 0.0858. This is multiplied by $\frac12\rho V^2A_F$ to get the drag.

The other forces and moments on the fuselage are usually not great, as the fuselage is not designed to produce these forces. For this report, I chose to neglect them. This is usually not a good assumption at all, especially for pitching and yawing moments.

The empennages are lifting surfaces, aerodynamically optimized to produce a force perpendicular to the incoming wind. This lift force is proportional to the angle of attack (or angle of sideslip for the vertical stabilizer).

The lift coefficient of the horizontal stabilizer is given by

$$C_{L_{(hs)}}=a_{hs}\alpha=a_{hs}\tan^{-1}\left(\frac{w-v_i}u\right)$$

and the coefficient of the vertical stabilizer by

$$C_{L_{(vs)}}=a_{vs}\beta=a_{vs}\sin^{-1}\left(\frac vV\right)$$

where $a_{hs}$ and $a_{vs}$ are the lift curve slopes of the horizontal and vertical stabilizers, respectively. The $v_i$ that appears in the angle of attack is the rotor downwash on the tail. The drag coefficient of either stabilizer is approximated by

$$C_D = C_{D_0} + \frac{C_L^2}{\pi AR e}$$

where $AR$ is the aspect ratio of the empennage, and $e$ is an efficiency factor that accounts for profile and induced drag effects at higher lift. The lift and drag forces are rotated into the body axes, and converted to dimensional form by multiplying by $\frac12\rho V^2S$, where $S$ is the planform area of the empennage.

Moments produced by the empennages themselves are small and negligible; however, the empennages are at long moment arms from the center of gravity. For example, the pitching moment of the horizontal stabilizer is given by $M_{hs} = Z_{hs}\times\ell_{hs}$, where $\ell_{hs}$ is the moment arm.