


Next: References
Up: Helicopter Dynamic Stability
Previous: Trim
Subsections
In stability analysis, we are interested in the helicopter's behavior
near its trim condition. We want to know whether small disturbances
tend to converge back to the trim state, or diverge and grow larger.
We do this by linearizing the equations of motion at the trim
condition. The solution to a linear set of equations is an
exponential. One can tell whether a particular mode converges or
diverges simply by looking at the exponents (eigenvalues): a positive
real part indicates divergence, while a negative real part indicates
convergence.
The traditional way to linearize the equations of motion is as
follows:
- 1.
- Write the state variables as a trim value plus a
perturbation value:
(The suffix 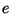 stands for equilibrium.)
stands for equilibrium.)
- 2.
- Linearize the aerodynamic forces and moments, by writing them as
first order Taylor-series expansions in state space. For example:
The stability derivatives are constant and evaluated at the trim
condition. Due to the complex nature of the force equations, the
stability derivatives are calculated using a central difference:
- 3.
- Linearize the Coriolis forces (terms such as
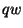 )
like this:
)
like this:
- 4.
- Assume that the Euler angles do not change much from their trim
value. Wherever
 and
and  appear in the equations of
motion, replace with
appear in the equations of
motion, replace with 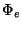 and
and 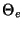 .
.
Once the equations are linearized, it is convenient to work in vector
notation. Define the state vector as
and write it as a trim value plus a perturbation value:
Then, if 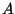 is a linear coefficient matrix for the linearized
equations of motion, the homogeneous equations (that is, the equations
with no control inputs) can be written in vector form as
is a linear coefficient matrix for the linearized
equations of motion, the homogeneous equations (that is, the equations
with no control inputs) can be written in vector form as
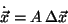 |
(2) |
For this report, I chose to determine the values of the coefficient
matrix in a nontraditional way. The equations of motion can be
thought of a multivalued function of the state variables, returning
the state variable rates. If 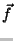 is the function, the full
(nonlinear) equations of motion can be written
is the function, the full
(nonlinear) equations of motion can be written
The linearization of vector function 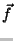 is simply
is simply
where 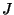 is the Jacobian matrix of
is the Jacobian matrix of 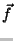 .
The components of the
Jacobian are calculated with finite difference approximations. (The
analogous scalar concept is to expand the state variable rates as
first-order Taylor series, using the equations of motion. For example:
.
The components of the
Jacobian are calculated with finite difference approximations. (The
analogous scalar concept is to expand the state variable rates as
first-order Taylor series, using the equations of motion. For example:
The derivatives in the above formulation are the components of the
Jacobian.)
There are several advantages to the second approach; the most
important is the savings in human time. Because it is vectorized, the
Jacobian matrix can be generated with a double loop. The traditional
linearization method requires calculation of stability derivatives
first, and then filling in the components of the matrix 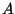 with
various expressions. Programming a loop requires much less programmer
time. On the other hand, the traditional method is more efficient
computationally.
with
various expressions. Programming a loop requires much less programmer
time. On the other hand, the traditional method is more efficient
computationally.
The solution to Equation 10 is
where 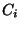 is the
is the 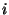 th arbitrary constant,
th arbitrary constant,
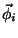 is the
is the 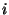 th
eigenvector, and
th
eigenvector, and 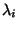 is the
is the 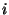 th eigenvalue.
th eigenvalue.
The stability characteristics of the solution are determined by the
eigenvalues; they hold information about the modes such as damping
ratio, time constants, and frequency of oscillation. Thus, the first
look at stability characteristics looks at the eigenvalues.
The set of eigenvalues obtained while varying one parameter over a
specific range is a root locus. For the helicopter, a useful root
locus plots the eigenvalues at different airspeed.
Figures 1-3 present the root loci of the
example helicopter given in Prouty.
Eigenvectors are used to determine the nature of the motion in a
particular mode. This enables one to determine what the modes in a
root locus are. An eigenvector that has a large value for  ,
but a very small value for the other variables, is a roll mode because
most of the motion is in rolling.
,
but a very small value for the other variables, is a roll mode because
most of the motion is in rolling.
Figure:
Root locus plot for example helicopter given in Prouty,
plotting eigenvalues at airspeeds from 0 to 200 ft/s. There are two
mode loci spanning the real axis: the roll mode at values less than
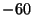 ,
a pitch mode between
,
a pitch mode between 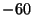 and
and 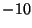 .
Both modes are heavily
damped. (In fact, they are so heavily damped I doubt their
correctness.)
.
Both modes are heavily
damped. (In fact, they are so heavily damped I doubt their
correctness.)
![\includegraphics[width=\textwidth]{rl1.eps}](img88.gif) |
Figure 2:
Zoomed root locus plot of the example helicopter. This shows
a curious mixture of modes. The bow shaped mode locus on the left is
a short-period pitch oscillation mode, and occurs in forward flight
but not hover. At low speeds, the mode locus intersects the real axis
and becomes two oscillatory modes: the pitch mode and a vertical
motion mode. On the right, there is another oscillatory mode, which
is the Dutch roll mode. It only seems to exist at high speeds; at low
speeds the mode divides into two non-oscillatory modes. (This is
very unexpected and yet another reason to doubt my results.) Also on
the real axis, intermeshed with the other modes, is the spiral mode.
It is not heavily damped, but is stable.
![\includegraphics[width=\textwidth]{rl2.eps}](img89.gif) |
Figure 3:
The root locus plot zoomed even further. This plot shows the
phugoid mode. It is an unstable mode, because its real part is
positive. At hover, the mode locus is at the right side of the plot,
and moves to the left at higher speeds. Even at high speed, the mode
is still slightly unstable.
![\includegraphics[width=\textwidth]{rl3.eps}](img90.gif) |



Next: References
Up: Helicopter Dynamic Stability
Previous: Trim
Carl Banks
1999-12-22
![]() is the function, the full
(nonlinear) equations of motion can be written
is the function, the full
(nonlinear) equations of motion can be written
![]() with
various expressions. Programming a loop requires much less programmer
time. On the other hand, the traditional method is more efficient
computationally.
with
various expressions. Programming a loop requires much less programmer
time. On the other hand, the traditional method is more efficient
computationally.
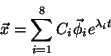
![]() ,
but a very small value for the other variables, is a roll mode because
most of the motion is in rolling.
,
but a very small value for the other variables, is a roll mode because
most of the motion is in rolling.
![\includegraphics[width=\textwidth]{rl1.eps}](img88.gif)
![\includegraphics[width=\textwidth]{rl2.eps}](img89.gif)
![\includegraphics[width=\textwidth]{rl3.eps}](img90.gif)