The polynomial models described above, as well as many other models, are single point models. Such models treat the aerodynamic forces and moments as point forces and moments acting through the reference point of the airplane. However, there are situations where it is useful to model distributed aerodynamic forces, because of the radical difference in conditions that appear in different parts of the aircraft in certain flight conditions. This can have drastic effects on the resultant aerodynamic force and moment. A spin is a good example of a flight condition where this occurs; among other things, the outer wingtip has a significantly higher airspeed than the inner wingtip due to the high yaw rate.
Because of their complexity, capturing these effects using a single point model is tricky. It can be done using enough terms. However, it is often to better to model phenomena as they really are. That is, if local variations in force cause complex behavior, it makes sense to consider these local variations, rather than to force single-point polynomials to model their effects.
A simple multipoint approach is to use a separate polynomial model for each lifting surface. Thus, the individual aerodynamic force and moment on the wing, horizontal tail, vertical tail, and fuselage is summed to yield the total aerodynamic force and moment. A slightly more complex model considers the left and right halves of each lifting surface separately. A still more complex model separates each lifting surface, and the fuselage, into lengthwise panels, calculating the force and moment produced by each panel. For example, the wing may consist of eight panels, the horizontal tail four, the vertical tail two, and the fuselage six.
The logical extreme of the multipoint model is to consider infinitely
thin panels. This can be done using strip
theory
![]() ,
where the resulting
force on a lifting surface is the integral of force per unit length
along the span. The force can be evaluated analytically by expressing
the components of the integral as Taylor-expanded polynomials. For
example, the lift of the right half of the wing could be represented
by Equation 61:
,
where the resulting
force on a lifting surface is the integral of force per unit length
along the span. The force can be evaluated analytically by expressing
the components of the integral as Taylor-expanded polynomials. For
example, the lift of the right half of the wing could be represented
by Equation 61:
| q(y) | = | 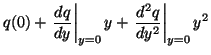 |
|
| = | 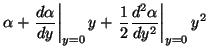 |
||
| = |
| (62) |
One problem with multipoint models is that they usually have a large number of parameters. The large number of parameters can lead to an ill-conditioned problem, very similar to the ill-conditioned problem of single-point polynomial models, making numerical parameter identification difficult. A possible remedy for this is to collect data on the distributed force, rather than just the resultant force.