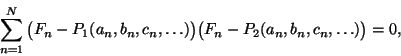More Complex Polynomial Models

The basic model described above has two restrictions. First, its domain of accuracy is small; it cannot correctly model flight conditions such as advanced stall and spins. Second, the basic model cannot simulate the many subtle effects (for example, how $C_{L_\beta}$ changes with angle of attack), because there are no terms to account for such effects. These subtle effects are small compared to lift versus angle of attack, and are not easy to calculate, and so they are not used in the basic model. However, these effects are real, and not accounting for them limits the maximum accuracy of the model.

The obvious solution to these problems is to use more terms in the polynomials. More terms can make the model more accurate, as well as increase its domain of accuracy. Unfortunately, as more terms are added, it becomes increasingly difficult to calculate the coefficients. Therefore, complex polynomial models use numerical methods of parameter fitting to determine the coefficients. The parameter fitting methods rely on test data (either from flight tests or wind tunnel tests).

However, before parameter fitting, one must choose which parameters are needed. One possibility is to use brute force; simply choosing any desired polynomial terms, and letting the optimizer decide whether there is any relationship of significance. This method is problematic for two reasons. First, the memory and computer time required for this is very large. Second, as the degree of the polynomials increase, it becomes increasingly likely that two terms may be nearly linearly dependent with the given test data $^{\ref{ref:morelli1}}$. This creates an ill-conditioned problem.

Reference 12 presents a method to determine a set of terms that are not linearly dependent. It derives a method of selecting terms that are orthogonal to each other based on the given data set. (Suppose there are N data points, with each data point listing the force F and the state variables $a,b,c,\ldots$ at some point in time. Two terms $P_1(a,b,c,\ldots)$ and $P_2(a,b,c,\ldots)$are orthogonal if

$$\sum_{n=1}^N \big(F_n - P_1(a_n,b_n,c_n,\ldots)\big) \big(F_n - P_2(a_n,b_n,c_n,\ldots)\big) = 0,$$

where the subscript n indicates the nth data point.) The method presented in Reference 12 does not yield polynomial terms; however, a well-conditioned polynomial can be derived from the orthogonal terms.