Manifold Pressure Calculation

Equation 65 presents the quasi-static differential equation for manifold pressure $^{\ref{ref:heywood}}$.

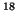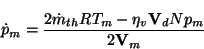$$\dot p_m = \frac{2\dot m_{th} RT_m - \eta_v \mathbf{V}_d N p_m}{2 \mathbf{V}_m}$$ (65)

For high speed engines, this equation could be numerically unstable with the simulator's time step size; in such cases, it is appropriate to ignore the transients by setting 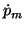$\dot p_m$ to zero and solving Equation 65 directly for p_m. (Reference 18 reports that the time constant of the Equation 65 is 2 to 4 times the length of an intake stroke. At 2400 RPM, twice the intake stroke is 0.025 seconds. A typical time step size for a flight simulator is 0.01 seconds.)

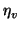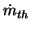In Equation 65, the volumetric efficiency $\eta_v$ is only weakly dependent on the manifold pressure; this paper assumes it to be independent of p_m. The manifold temperature T_m is assumed known; an adequate estimate is to use outside air temperature. V_d and V_m are constants for the engine, and N is the engine speed. Only $\dot m_{th}$ is left to be determined.

If p_m > 0.528p, then the flow is not choked at the throttle. The mass flow rate past the throttle is given by Equation 66 $^{\ref{ref:heywood}}$:

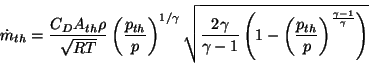$$\dot m_{th} = \frac{C_D A_{th}\rho}{\sqrt{RT}} \left(\frac{p... ...ft(\frac{p_{th}}{p}\right)^{\frac{\gamma-1}{\gamma}} \right)}$$ (66)

The coefficient of discharge C_D in Equation 66 is an empirical, engine-dependent parameter, which accounts for the pressure loss due to all of the obstacles in the intake (air filter, throttle, venturi, etc.). It is a function of the engine speed and throttle plate open area. One can obtain a first-order estimate of C_D by setting it so that Equation 65 yields the observed manifold pressure drop at steady state with a wide-open throttle at a high engine speed. p_th is the pressure at the throttle. It is not clear from Reference 18 how to determine this; however, it seems that, although technically invalid, the manifold pressure is used for p_th.

If p_m < 0.528p, then the flow is choked at the throttle. In this case, mass flow rate is given by Equation 67 $^{\ref{ref:heywood}}$:

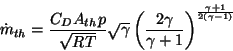$$\dot m_{th} = \frac{C_D A_{th} p}{\sqrt{RT}}\sqrt{\gamma} \left(\frac{2\gamma}{\gamma+1}\right)^\frac{\gamma+1}{2(\gamma-1)}$$ (67)