| CT | 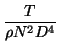 |
(68) | |
| CP | 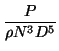 |
(69) | |
| J | (70) |
Many thrust and power calculations use nondimensional parameters;
these are defined by Equations 68-70.
Propeller efficiency charts, which are useful in performance analysis of steady, level flight, are not sufficient for flight simulation. The reason is that, in performance calculations, thrust is considered equal to drag. This is not true in general for a flight simulator.
Therefore, to model the propeller, one needs to determine the thrust produced. The thrust produced by the propeller is a function of the forward airspeed, the air density, the blade geometry (including the variable pitch setting), and the propeller's angular speed. The thrust can be calculated with a theory such as blade-element theory or vortex theory. One can also use empirical data (such as the chart on Page 306 of Reference 7) to determine the thrust.
Once the thrust is determined, the power consumed by the propeller can
be found using the propeller efficiency charts in tabular form, by
solving the following relation for CP:
Note that the power consumed by the propeller does not necessarily equal the power delivered to it by the engine. Any excess power delivered through the shaft increases the propeller's angular speed. Similarly, if the propeller does not receive enough power from the engine, its angular speed decreases.
Newton's Second Law for angular momentum, applied to the propeller, is
![]() .
The excess power is related to the propeller
torque by the relation
Pe = Qp N. Combining the two equations
yields the differential equation for engine speed:
.
The excess power is related to the propeller
torque by the relation
Pe = Qp N. Combining the two equations
yields the differential equation for engine speed:
Assuming the shaft axis is parallel to the body x-axis, and lies in
the x-z-plane, the propulsive force and moment components are: